Mikis' Bookmarks

È da anni che voglio spendere due parole sull’uso dell’espressione “crescita esponenziale”; la cronaca di questo periodo mi costringe a buttare il cuore al di là dell’ostacolo e dedicare qualche riga all’argomento.

Succede abbastanza spesso sentire persone che parlano di crescita esponenziale per indicare una crescita rapida: “la nostra azienda, negli ultimi anni, ha avuto una crescita esponenziale”, “abbiamo visto una crescita esponenziale delle richieste dei nostri clienti” e altre frasi di questo tipo, intendendo un successo dell’attività o di un prodotto che magari è cresciuto del 20, 30 o magari anche del 50% in 2 o 3 anni.

Facendo una semplice ricerca in rete prendo alcuni articoli a caso:

• Crescita esponenziale per il mercato dell’accumulo energetico (su elettricomagazine del 31 Marzo 2020)
• Crescita esponenziale nel nostro Paese di vendite per uso domestico di tapis roulant (su ilrestodelcarlino del 29 marzo 2020)
• Crescita esponenziale e tante novità per l’associazione “Passione Pappagalli Free Flight” (su wuoow.com del 9 Marzo 2020)

Capisco che il linguaggio comune si possa prendere delle libertà, ma da un punto di vista matematico l’espressione usata in quel modo è decisamente sbagliata.

Il grafico, preso in prestito da Wikipedia, mostra differenti funzioni di crescita, fra le tante che esistono:
– crescita lineare (in rosso)
– crescita cubica (in blu)
– crescita esponenziale (in verde)

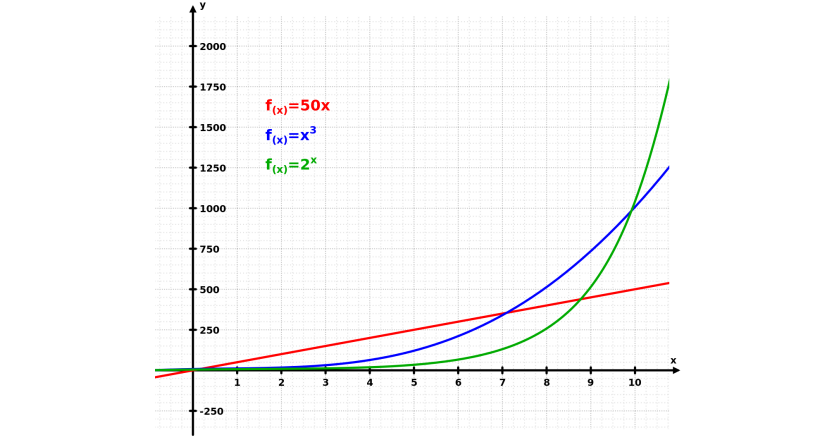
Come viene visualizzato dal grafico, non in tutti i punti la crescita esponenziale è la funzione di crescita più veloce. Ad esempio, all’inizio, sia la crescita lineare che quella cubica possono risultare più veloci della crescita esponenziale.

La crescita esponenziale infatti non è caratterizzata da una crescita veloce. Al contrario, all’inizio presenta una crescita lenta, ma che poi mostra un’accelerazione tanto improvvisa quanto potente.

Da un punto di vista prettamente matematico, in una funzione lineare la variabile indipendente (x) ricopre il ruolo di fattore moltiplicativo, mentre in una funzione esponenziale la variabile indipendente compare ad esponente.

funzione lineare: y = b • x
funzione esponenziale: y = b^x

Una grandezza cresce esponenzialmente quando ad intervalli di tempo uguali corrispondono incrementi pari ad una frazione costante del totale. Considerando che il tempo non smette mai di crescere, vuol dire che ciò che cresce in maniera esponenziale tende a diventare infinito.
Bisogna comunque tenere conto che generalmente i fenomeni che sono caratterizzati da una crescita esponenziale, lo sono solo per un determinato, limitato, periodo di tempo.

A tal proposito ci sono un paio di noti esempi, generalmente proposti sotto forma di indovinello, che spesso si usano per mostrare crescite esponenziali; per inciso entrambi hanno al loro interno una limitazione che evita la crescita infinita.

La ninfea nello stagno
In uno stagno c’è una bellissima ninfea, che ogni giorno raddoppia la propria estensione e in 30 giorni copre tutto lo stagno. Quanto tempo impiega per coprirne la metà?

La risposta è 29 giorni: infatti il giorno seguente -il trentesimo- raddoppierà coprendo l’intero lago.

Riso e scacchiera
Una leggenda narra che nel 600 d.C., un Imperatore Indiano, che amava molto gli scacchi, decise di dare una ricompensa al contadino che aveva inventato il gioco e gli disse che popteva essere ricompensato con ciò che desiderava.
Il contadino chiese di ricevere un chicco di riso per il primo quadrato della scacchiera, due per il secondo, quattro per il terzo, otto per il quarto e così via, raddoppiando ogni volta.
L’imperatore pensò che la richiesta fosse irrilevante ed ordinò immediatamente al suo tesoriere di dare seguito alle richieste del contadino.
Dopo un’intera settimana, tanto impiego il tesoriere per calcolare quanto riso fosse necessario per fare fronte alla richiesta del contadino, si accorse che non vi era possibilità onorare il debito.
Infatti, un chicco di riso che raddoppia consecutivamente per 64 volte (tanti sono i quadrati della scacchiera) dà come risultato 18.446.744.073.709.551.615 chicchi di riso.
L’imperatore non ne aveva a sufficienza.